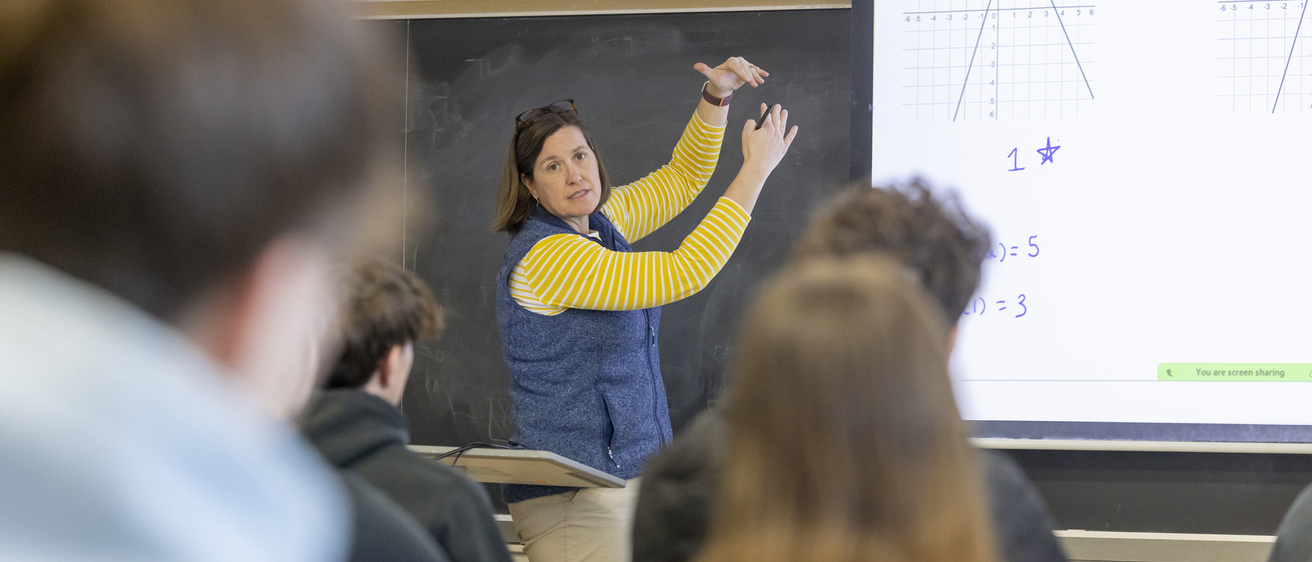Mathematics | College of Liberal Arts and Sciences

$math students at a black board working on calculations$

Shape the future with mathematics

Challenge yourself, conduct impactful research, and develop a versatile skill set for a successful career using mathematics.

Apply Now Visit Campus Request Info

Why Iowa?

Study mathematics at Iowa where you will develop problem-solving skills, critical thinking, and help shape the future through innovation and discovery.

Study Here

$math students in classroom$

Find your path

Learn skills that will prepare you for many careers in industry, education, and mathematical research or for graduate school.

Find your path

$math students on the pentacrest discussing math problems$

Advance your work

Develop your skills as a researcher and educator. Join a program with a 100 percent job placement record.

Advance your work

$CIndy Farthing teaching math class in front of white borad with math equations$

Learn from experts

Our faculty are professionals and conduct research in several areas, including algebra, analysis, differential geometry, and more.

Learn from experts

See yourself here

Study mathematics at Iowa, where innovative research, dedicated faculty, and a vibrant academic community will help you succeed.

Visit

$Portrait of Astra Tomas$

"The professors in the math department are always able to help you when you are stuck and are eager to direct you on pathways to future success. The TAs in the math lab are always working in order to help your understanding and to help provide insight."
- Astra Tomas

Write Your Story

Build knowledge. Conduct research. Stand out. Our graduates go on to have fulfilling careers in industry, education, and mathematical research.

Apply

$student wearing Iowa sweatshirt rasing her hand to anser questions in math class$

100%

Job placement for graduate students

$students in math class working together on a problem$

30

faculty members

4,000

undergraduate students taught each semester

(2018-2020 data)

$close up of math problem on ipad$

Tutoring

Our Math Tutorial Lab is here to support you.

$Cinday Farthing teaching$

News and announcements

Marge Murray receives Hubbard-Walder Award for Excellence in Teaching

Friday, April 26, 2024

Adriana Fernandez Quero wins 2024 CLAS Dissertation Writing Fellowship

Thursday, February 22, 2024

Department of Mathematics graduate student Adriana Fernandez Quero won a 2024 CLAS Dissertation Writing Fellowship.

Midwest Numerical Analysis Day conference set for April 13-14, 2024

Tuesday, February 20, 2024

The University of Iowa will host the Midwest Numerical Analysis Day 2024 conference in April 2024.

Mathematics faculty member Cindy Farthing receives CLAS Collegiate Teaching Award

Thursday, November 30, 2023

Cindy Farthing, and her husband Fred Boehmke each received a CLAS Collegiate Teaching Award, which is presented annually to faculty members who show exemplary performance in their work.